티스토리 뷰
1. 문제 링크
https://www.acmicpc.net/problem/1006
1006번: 습격자 초라기
하나의 특수 소대로 인접한 두 영역을 커버할 수 있는 배치는 (2,10), (9,16), (4,5), (7,8), (13,14) 이다. 그리고 나머지 6개 구역은 각각 하나의 특수 소대로 커버할 수 있다. 그러므로 최소 11개 특수 소�
www.acmicpc.net
2. 문제 개요
초라기는 각각 W명으로 구성된 특수 소대를 다수 출동시켜 모든 구역에 침투시킬 예정이다. 특수 소대를 배치하는 데는 여러 조건이 있다.
원타곤의 모든 구역을 커버하기 위해 침투시켜야 할 특수 소대의 최소 개수를 출력하는 프로그램을 만들자.
3. 문제 힌트
문제를 곰곰히 생각해보면 타일링 문제와 상당히 비슷함을 알 수 있다. 단 원형이라는 조건과, 적의 인원수에 따라서 2칸을 커버할 것인지, 1칸을 커버할 것인지에 대한 조건이 추가되었다는 점이다.
일단 문제를 해당조건 중 원형이라는 조건을 제외하고 생각해보자.
(1) 선형이라고 가정하고 문제를 풀었을 때, 어떻게 dp 식을 세울 수 있을까?
(2) 인접한것 중 2개를 커버할 수 있다. 커버할 수 있다면 무조건 커버해야 할까?
개수의 최적화(최소)를 위해서는, 2칸으로 묶을 수 있다면 묶어주어야 한다. 그래야 최솟값을 항상 가지고 감을 보장해준다.
2칸을 만들 수 있는데 묶지 않고 놔둔다고 가정하자. 그럼 최적값을 구할 수 있을까?
물론
| 1 | 30 | 71 |
| 100 | 70 | 71 |
여기서 한계치는 100이라고 해보자,
(1,30)을 묶어 버린다면 나머지 71, 71, 70, 100들은 혼자 있어야 하고, 5개가 된다.
그런데 (1,30)을 묶지않고 (1,71), (30,70)을 묶는다면 4개 만에 해결할 수 있다. 이런 경우는 존재한다. 하지만 이런경우는 dp로 구해나가면서 경우의 수를 살필 때 처리해주는 부분이다.
4. 문제 풀기
처음에 문제를 간단히 생각해보려고 했다. 곰곰이 생각해보니 타일링 문제랑 상당히 비슷하다고 느꼈고, 일단 선형으로 먼저 풀어보자고 생각했다.
이 문제에서 특별한 점은 1x1타일이 있다는 점이라고 생각해도 되겠다.
3가지의 상태가 있다. 왜냐하면 열이 2열이 최대이기 때문이다.
i) 위아래를 모두 고려하는 경우
ii) 아래만 고려하는 경우
iii) 위만 고려하는 경우
여기서, 위아래를 모두 고려하는 경우는 모두 고려하지않는 경우와 겹친다. 예를들면, n-1행까지 했을때, 모두 고려하는경우와 n행까지 했을때 모두 고려하지 않는경우와 겹친다. 따라서 상태수를 줄였다.
dp 식을 세우기에 앞서 설계를 해보자,
dp[n][3]으로 나타낼 수 있겠다.
여기서 첫 번째 원소는 n번째 행까지 고려했을 때를 나타낸다.
[3]은 상태가 된다. [0]인 경우는 i)의 경우, [1]은 ii), [2]는 iii)의 경우가 된다.
(1) 위, 아래를 모두 고려하는 경우
dp[n][0] = ~~. 여기서 ~~를 보자.
어떤 상태에서 n번째 행에서 모두 고려(커버) 할 수 있는 경우로 도달할 수 있을까?
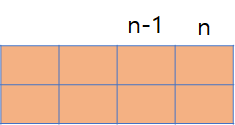
다음과 같은 4가지의 경우에서 목표 경우로 도달할 수 있다.
i) dp[n-1][0] + 세로 1개 or 2개
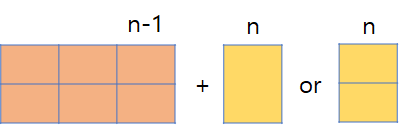
ii) dp[n-2][0] + (위, 아래 각각) 가로 1개 or 2개

이경우에는 4가지가 올 수 있다. 모두 1개 1개 1개 1개로 분할되는 경우,
위 1개 밑 2개, 밑 1개 위 2개, 위 1개 밑 1개와 같은 경우이다.
iii) dp[n-1][1] +(위) 1개 or 2개 +(밑) 1개
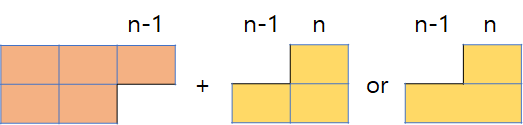
iiii) dp[n-1][0] + (밑) 1개 or 2개 + (위) 1개
이 경우는 iii)과 반대의 경우이다.
(2) 밑에만 고려하는 경우

위의 목표처럼 도달하기 위해서는,
i) dp[n-1][2] + (밑) 1개 or 2개
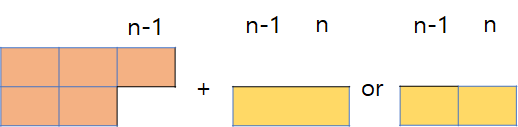
ii) dp[i-1][0] + (위) 1

이번 경우는 1개 or 2개가 아니고 무조건 1개가 온다는 것이 특이하다.
(3) 위에만 고려하는 경우
(2)와 비슷하다.
이런 점을 고려해서 선형적으로 구하는 DP를 작성하자.
그럼 이제 어떻게 환형인 경우를 구할 수 있을까 잘 생각해보자.
선형으로 구했다는 것은, 환형으로 연결이 되지 않은 경우이다.
즉 1 번열과 n번째 열이 서로 아무 관계가 없다는 의미이다.
이 처럼, 환형으로 연결되는 것은 4가지로 구분 지을 수 있다.
아무것도 연결되지 않는 경우
위만 연결되는 경우
밑만 연결되는 경우,
위, 밑 둘 다 연결되는 경우,
이 4가지를 dp함수를 돌리기 전에 미리 설정해놓고 4가지 경우중 가장 작은 것을 선택하도록 한다.
이해를 위해 예를 들어보면,
만약에 위에만 연결된다고 가정해보자, 이렇게 사전처리를 해주는 의의는
나는 마지막 열의 위와, 처음 열의 위를 억지로 연결시킬 거고, 이게 연결된 경우의 최솟값을 구할 거야.라고 생각할 수 있겠다.
따라서 억지로 연결해 준부분을 dp함수에 의해 다른 인접한 구역들과 묶이지 않도록 해야 하고 따라서,

위의 사진처럼 했다. 위의 사진은 dp[n][1]과 같은 경우이다.
묶었다 라는 경우는 어차피 1개이고, 마지막 열의 윗부분을 고려하는 것과, 안 하는 것과 값은 어차피 동일하다.
이게 헷갈린다면,

이렇게 두고 dp[n][0]를 구한다면, 2개의 INF들은 1개로 묶인 상태이지만, INF로 둔다면, 묶이지 않고 각각 처리하는 것처럼 dp함수는 구할 것이다.
따라서 dp[n][0] - 1을 해주면, 묶인 것처럼 나타내 줄 수 있겠다.
5. 코드
#include <cstdio>
#include <cstring>
#include <algorithm>
#define INF 987654321
using namespace std;
int arr[2][10001];
int dp[10001][3];
int n, w;
void solve()
{
for (int i = 2; i <= n; ++i) {
int up = arr[0][i - 1] + arr[0][i] <= w ? 1 : 2;
int down = arr[1][i - 1] + arr[1][i] <= w ? 1 : 2;
int ver = arr[0][i] + arr[1][i] <= w ? 1 : 2;
dp[i][0] = min({ dp[i - 1][0] + ver, dp[i - 2][0] + up + down,dp[i - 1][1] + up + 1,dp[i - 1][2] + 1 + down });
dp[i][1] = min(dp[i - 1][2] + down, dp[i - 1][0] + 1);
dp[i][2] = min(dp[i - 1][1] + up, dp[i - 1][0] + 1);
}
return;
}
int main()
{
int t;
scanf("%d", &t);
while (t--)
{
memset(dp, 0, sizeof(dp));
scanf("%d %d", &n, &w);
for (int i = 0; i < 2; ++i)
for (int j = 1; j <= n; ++j)
scanf("%d", &arr[i][j]);
int t_up = arr[0][1];
int t_down = arr[1][1];
int ans = INF;
//연결안된경우
dp[1][0] = arr[0][1] + arr[1][1] <= w ? 1 : 2;
dp[1][1] = dp[1][2] = 1;
solve();
ans = min(ans, dp[n][0]);
//위에거 연결 되는경우2
if (arr[0][1] + arr[0][n] <= w) {
//memset(dp, 0, sizeof(dp));
dp[1][0] = 2;
dp[1][1] = dp[1][2] = 1;
arr[0][1] = INF;
solve();
ans = min(ans, dp[n][1]);
arr[0][1] = t_up;
}
//밑에거 연결 되는경우1
if (arr[1][1] + arr[1][n] <= w) {
dp[1][0] = 2;
dp[1][1] = dp[1][2] = 1;
arr[1][1] = INF;
solve();
ans = min(ans, dp[n][2]);
arr[1][1] = t_down;
}
//둘다 연결되는경우0
if (arr[0][1] + arr[0][n] <= w && arr[1][1] + arr[1][n] <= w) {
arr[0][1] = arr[1][1] = INF;
dp[1][0] = 2;
dp[1][1] = dp[1][2] = 1;
solve();
ans = min(ans, dp[n - 1][0]);
arr[0][1] = t_up;
arr[1][1] = t_down;
}
//단 1개인 경우 고려하기
if (n == 1)
ans = arr[0][1] + arr[1][1] <= w ? 1 : 2;
printf("%d\n", ans);
}
return 0;
}6. 결과 사진

지적, 댓글 언제나 환영입니다~
'알고리즘 > Dynamic Programming' 카테고리의 다른 글
| boj, 백준) 1949. 우수 마을 ( C / C++) (0) | 2020.06.05 |
|---|---|
| boj, 백준) 2306. 유전자 ( C / C++) (0) | 2020.06.05 |
| boj, 백준) 2342. Dance Dance Revolution ( C / C++) (0) | 2020.05.29 |
| 백준, boj) 2482. 색상환 ( C / C++ ) (0) | 2020.05.26 |
| 백준, boj) 1509. 팰린드롬 분할 ( C / C++) (0) | 2020.05.23 |
